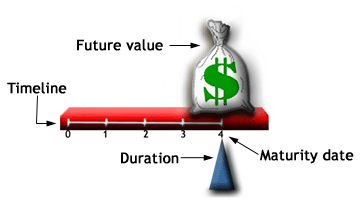
A Duration é uma medida de tempo médio ponderado de
recebimento/pagamento dos fluxos de caixa de um título.
São 3 tipos básicos de duration, conforme já visto no quadro anterior. Agora vamos entender as suas aplicações com exemplos.
Duration de Macaulay:
• Dados
para aplicação da Duration de Macaulay em um exemplo:
• Valor
de face do título de renda fixa: R$ 1.000,00
• Maturidade
do título: 3 anos
• Taxa
de juros: 4% a.a.
• Cupom:
5% a.a.
• Fluxos
de caixa esperados:
• Ano
1 = R$ 50,00
• Ano
2 = R$ 50,00
• Ano
3 = R$ 50,00 + R$ 1.000,00 = R$ 1.050,00
• Resultado:
• Preço
do título = R$ 1.027,75
Duration de Macaulay = 2,86 anos
Duration Modificada:
• Dados
para aplicação da Duration Modificada:
• Maturidade
do título: 3 anos
• Taxa
de juros: 4% a.a.
• Cupom:
5% a.a.
• Preço
do título: R$ 1.027,75
• Duration
de Macaulay: 2,86 anos
• Resultado:
• Duration
Modificada = 2,75 anos
• O
que acontece em cada situação?
• Se
a taxa de juros sai de 4% para 5%?
• Se
a taxa de juros sai de 4% para 3%?
Duration Efetiva:
• Preço
se a taxa de juros cair para 3% (com opção de recompra): R$ 1.019,42
• Preço
se a taxa de juros subir para 5%: R$ 1.000,00
• Duration efetiva: 0,945 anos.
A convexidade é uma métrica financeira que vai além da
Duration ao avaliar o comportamento de um título frente às mudanças nas taxas
de juros. Enquanto a Duration oferece uma visão linear da relação entre taxas
de juros e preço do título, a convexidade introduz uma dimensão adicional que
considera o "formato" ou a "curvatura" dessa relação. Em
outras palavras, a convexidade captura como a sensibilidade do preço de um
título às taxas de juros pode mudar à medida que essas taxas mudam.
Por que a Convexidade é Importante?
- Precisão
na Estimativa: A Duration fornece uma boa aproximação da mudança no
preço de um título para pequenas variações nas taxas de juros. No entanto,
para mudanças maiores, a convexidade pode oferecer uma estimativa mais
precisa.
- Mitigação
de Riscos: Títulos com alta convexidade são menos sensíveis a
flutuações nas taxas de juros, o que os torna menos arriscados. Assim,
eles podem ser usados para mitigar riscos em um portfólio.
- Oportunidades
de Lucro: Uma alta convexidade também pode ser vantajosa em ambientes
de taxas de juros voláteis, permitindo que os investidores se beneficiem
de mudanças tanto para cima quanto para baixo nas taxas.
- Diversificação
de Portfólio: Compreender a convexidade ajuda na construção de um
portfólio de títulos mais robusto e bem diversificado, que pode suportar
diferentes cenários de taxas de juros.
- Complemento
à Duration: A convexidade é frequentemente usada em conjunto com a
Duration para fornecer uma visão mais completa do perfil de risco de um
título. Combinar as duas métricas pode oferecer uma análise mais rica e
matizada.
• Dados
para aplicação da Convexidade:
• Valor
de face do título de renda fixa: R$ 1.000,00
• Maturidade
do título: 3 anos
• Taxa
de juros: 4% a.a.
• Cupom:
5% a.a.
• Resultado:
• Convexidade
= 10,41
• Pode
ser considerada moderada
• E
se a taxa de juros variar?
• Taxa
sobe para 5%, preço do título cai 2,70%, para R$ 1.000,01
• Taxa
cai para 3%, preço do título sobe 2,80%, para R$ 1.056,56
A Convexidade também pode ser usada na gestão de riscos e
até mesmo na otimização de carteiras:
- Convexidade
como Medida de Risco:
- A
convexidade é uma métrica-chave que permite aos gestores de portfólio
avaliar a sensibilidade dos títulos às variações nas taxas de juros de
forma mais completa do que a Duration sozinha.
- Mitigação
de Riscos:
- Títulos
com alta convexidade são úteis para mitigar o risco de taxa de juros,
pois são menos sensíveis a mudanças nas taxas.
- Ideal
para investidores que buscam preservar capital em cenários de taxas de
juros voláteis.
- Otimização
de Portfólio:
- A
convexidade pode ser usada para construir portfólios que maximizam o
retorno para um determinado nível de risco.
- Em
estratégias de "barbell", por exemplo, a convexidade total do
portfólio é aumentada pela inclusão de títulos com maturidades muito
curtas e muito longas.
- Convexidade
e Outras Formas de Risco:
- Além
do risco de taxa de juros, a convexidade também pode ter implicações para
outros tipos de risco, como o risco de crédito e o risco de liquidez.
- Considerações
Finais:
Entender a convexidade é crucial para a gestão eficaz de portfólios, especialmente para investidores com horizontes de tempo mais longos ou em ambientes de mercado incertos.
Embora a convexidade seja uma ferramenta valiosa, ela deve
ser usada em conjunto com outras métricas e análises para uma visão mais
completa do perfil de risco de um título ou carteira.
- Limitações
Matemáticas:
- A
convexidade é uma aproximação de segunda ordem que se torna menos precisa
para grandes variações nas taxas de juros.
- Títulos
com Opções Embutidas:
- Para
títulos "callable" ou "putable", a convexidade pode
ser negativa e a sua interpretação torna-se mais complexa.
- Custo:
- Títulos
com alta convexidade geralmente têm um custo maior, o que pode não ser
adequado para todos os investidores.
- Foco
Excessivo em Taxas de Juros:
- A
convexidade, como a Duration, está focada principalmente no risco de taxa
de juros, podendo negligenciar outros riscos como crédito e liquidez.
- Complexidade
Computacional:
- O
cálculo da convexidade pode ser mais complexo e demorado, especialmente
para títulos com fluxos de caixa irregulares ou opções embutidas.
Imunização é uma estratégia de gerenciamento de portfólio
que visa minimizar o impacto das flutuações nas taxas de juros sobre o valor
dos ativos e passivos.
- Como
Funciona: Ela envolve o ajuste da Duration e, em alguns casos, da
Convexidade dos ativos para que se igualem às dos passivos, ou
vice-versa.
- Objetivo
Final: O objetivo é tornar o valor líquido do portfólio insensível às
mudanças nas taxas de juros.
Importância da Imunização na Gestão de Riscos:
- Equilíbrio
de Ativos e Passivos: A imunização é vital para empresas e fundos que
precisam equilibrar ativos e passivos de longo prazo, como seguradoras e
fundos de pensão.
- Mitigação
do Risco de Taxa de Juros: Ajuda a proteger contra a volatilidade das
taxas de juros, que é uma das principais fontes de risco no mercado de
títulos.
- Estabilidade de Retornos: Ao minimizar a exposição às flutuações nas taxas de juros, a imunização pode ajudar a gerar retornos mais estáveis.
Na imunização por duration, é preciso ajustar as durations dos ativos da carteira para que ela seja
igual à duration dos passivos, de modo a mitigar a sensibilidade da carteira a
pequenas variações nos juros.
• Igualando
a Duration dos ativos e passivos:
• Cenário:
fundo de pensão com 3 títulos diferentes na carteira, com valor de R$ 1.000,00
cada. A Duration dos títulos é de 5, 6 e 10 anos.
• Duration
média dos ativos = 7 anos
• Os
passivos também têm Duration de 7 anos
• Neste
caso, a carteira já está imunizada para pequenas variações na taxa de juros. Caso fosse diferente, poder-se-ia ajustar as durations comprando ou vendendo títulos.
Além de levar em conta a Duration dos ativos e passivos,
considera a Convexidade para otimizar a gestão dos recursos, ajudando a
controlar melhor o desempenho da carteira em cenários mais voláteis.
• Quando
usar a Imunização por Convexidade?
• Cenários
voláteis
• Carteiras
mais complexas
Voltando ao mesmo exemplo do fundo de pensão:
• Ativos:
•
Duration = 6 anos
•
Convexidade = 25
•
Valor total = R$ 3.000
• Passivos:
•
Duration = 7 anos
•
Convexidade = 30
•
Valor total = R$ 3.000
• Necessidade
de ajustes:
•
Diferença de Duration = 1 ano
•
Diferença de Convexidade = 5
• Ajuste
de Duration:
•
Compra de um título de R$ 1.000, com 8 anos de
Duration e Convexidade de 35.
•
Nova Duration será de 6,5 e a Convexidade será
de 27,5
• Ajuste
de Convexidade:
•
Montagem de uma operação com um derivativo com
Convexidade de 50 e Duration 0.
• Imunização:
•
Dessa forma é possível Imunizar melhor a
carteira.




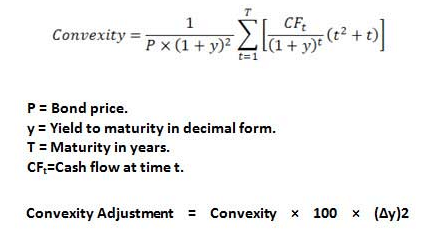
Nenhum comentário:
Postar um comentário